Moving Averages
A moving average is a type of trendline that smoothes out values of adjacent statistical observations and thereby eliminates minor or irregular fluctuations (called "noise"). A moving average is one of the most widely used technical analysis tools in all of trading, and serves as a workhorse indicator for many in the industry. In the most general sense, moving averages are used to identify trends in the market or in individual equities, with the ultimate goal of establishing positions in the direction of the trend.
While there are numerous methodologies for calculating moving averages, we will deal with the three most commonly used -- simple, weighted, and exponential. All of these calculations are based on the equity's closing price for the time frame used (e.g. daily, weekly, or monthly), with the idea being that there are many intra-period battles going on in the market and the war isn't won until the close. Some studies will base their calculations on intraday spreads between high and low pricing, but we will not pursue that issue here.
For the sake of example, we'll use a 10-day moving average throughout this discussion, though the calculations for weekly and monthly moving averages would follow the same logic.
Simple Moving Average
A simple 10-day moving average consists of successive averages of the 10 most recent trading days' closing values. The calculation is very straightforward: Simply add up the daily closing values and divide the sum by 10. With each subsequent day, the newest closing value is incorporated into the average and the value from 10 days previous is dropped.
The table below depicts closing prices for ABC Company on the dates indicated. The "First Series" column covers the 10 trading days from June 8 through June 21. First, we add the closing prices, which results in a sum of 698.45. Next, we divide this sum by 10 to yield ABC's 10-day moving average of 69.85 as of the market close on June 21.
Moving to the "Second Series" chart, note that we dropped the oldest reading of June 8 and replaced it with the June 22 closing value. The 10-day sum decreased to 694.09, resulting in a new 10-day moving average of 69.41.
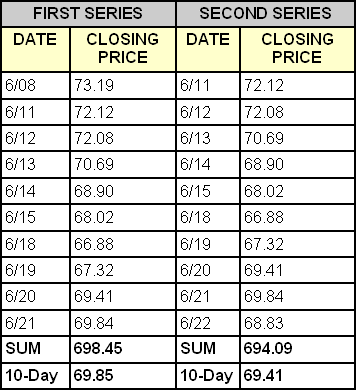
One of the objections some have with the simple moving average calculation is that it assigns equal weight to each of the 10 values. It is not unreasonable to argue that the most current readings should be more important as a reflection of what the stock is doing now. This takes on added importance as the time frame increases (e.g., from 10 days to 20 days). Since the calculation is modified each day by swapping out the oldest value in favor of the most current one, its fluctuation is a function of just those 2 numbers. That is, if the current value is greater than the one being dropped, the average turns upward. The converse is also true – if the current stock value is lower than that of 10 days ago, the average moves lower. This theory is demonstrated by the table above: When the June 8 value of 73.19 was dropped out and the June 22 value of 68.83 was added in, the result was a lower plot point for the 10-day moving average.
Weighted Moving Average
Although the process for calculating a weighted average is generally the same as that used for a simple moving average, there is one primary difference: More significance, or weight, is added to the most current readings. In the chart below, note that we have assigned weightings so that day 10 carries 10 times more significance than day 1.
The weightings may be allocated to suit the individual analyst's taste, and don't necessarily have to be uniformly progressive (e.g., 10, 9, 8, 7, and so on). The importance here is that you are consistent in your application. For example, there is no reason why the first 5 days cannot have equal weightings, with the progression occurring in days 6 through 10 (aside from the fact that you would be complicating an already cumbersome calculation, of course!).
The next step is to multiply the predetermined weighting by the day's closing price to come up with a weighted price. For this example, we have used the same ABC Company values from the "Second Series" column in the table above. The sum of the weighted price column is 3788.71. Next, we divide this figure by the sum of the weightings (here, 55) to arrive at a weighted 10-day moving average of 68.89. Note that this weighted 10-day plot point is lower than the plot point of the simple 10-day moving average, because more gravity is placed on the latter, lower readings.

Exponential Moving Average
Like weighted moving averages, this form of moving average assigns greater relevance to more current values. An exponential system is based upon the assignment of a fixed percentage weight to the current price – let's say 18%, though it could be any weighting (see below for rationale). All of the remaining weight (in this case, 82%) is then assigned to the previous value of the moving average itself. The proportional weight assigned to the most recent reading is often called a "smoothing constant."
To determine an exponential smoothing constant roughly proportional to a simple moving average of a given time length, divide the number 2 by one more than the length of the simple moving average you wish to replicate. This process may sound confusing, so let's look at an example. To find a smoothing constant to construct an exponential moving average comparable to a simple 10-day moving average, divide 2 by 11 (the number 11 being 1 more than the 10-day simple). The result is 0.18, which is why we chose an 18% weighting for the current price in this example.
As a starting point, let us assume day 1 to be the exponential moving average for that point in time. The exponential moving average is updated by multiplying the newest price by 0.18 (our smoothing constant) and adding that to the product of the previous exponential moving average multiplied by 0.82 (the balance of the 100% allocation). Staying with our ABC Company example, the results are shown in the table below.

Looking at the results from our 3 different types of moving averages, the largest spread between them is 0.52 points – or, just 0.75% of the simple 10-day moving average. So, is the additional work in calculating the weighted and exponential moving averages justifiable in terms of providing a trading edge? Note that the exponential trendline seems to react more quickly than the simple moving average, which could possibly signal a quicker entry or exit point for a trade.
We recommend that, no matter which type of moving average you use, stay consistent with that method. Bouncing from a simple to a weighted average will only confuse you, and restrict your ability to recognize equities that have historically reacted well around these trendlines.
Time Frames
We commonly use 10-unit and 20-unit simple moving averages. Unit refers to the time frame you wish to use, whether it be daily, weekly, or monthly. The different perspectives afforded by viewing an equity's progress over different time periods can be likened to taking a drive in the Rocky Mountains.
First, from a great distance, the range appears to be one solid piece of rock emanating from the earth's crust (comparable to viewing a long-term, or monthly, chart on a stock). Then, as you get a little closer – as with a weekly chart -- you start to notice that what first appeared to be a barren landscape is actually covered with trees and huge fields of snow. Next, taking a tram up the mountainside (or looking at a daily chart), you notice pastures of grass surrounding the tree line, an occasional lake nestled into a flat, not to mention a plethora of wildlife. This short-term, or daily, chart reveals things you could only imagine from the long-term perspective.
Each perspective provides you with a different viewpoint, though each independently does not afford a complete assessment of the mountain. Such is the reasoning behind examining the various chart views and their accompanying moving averages as parts of a whole.
Summation
There is no perfect moving average style or length. You could probably back-test all sorts of combinations and make a positive case for their predictive reliability for some stock or index. Ultimately, the ideal combination is the one that has worked for you. This brings us back to the concept of consistency. Whatever calculation or duration you use, make it yours and stick with it. Only repetitive trial and error will help you hone your technical skills with respect to moving averages.